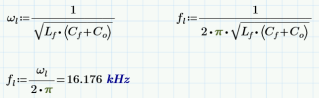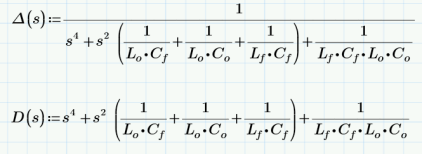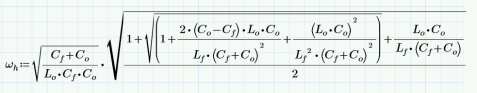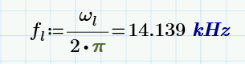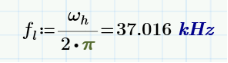[導讀]BUCK電路輸出一般只需要一級LC濾波器，精品計 根據傳遞函數得知,會產生兩個極點和180°相移，原創有老對于干擾噪聲有-40dB/10dec的兩級濾波路設衰減能力。對于特定產品在RE測試時候，器電尤其是司機車載產品，RF的精品計限定標準嚴苛，濾波效果不好，原創有老很容易下高頻處超標。兩級濾波路設

出品?21ic中國電子網??kk的器電回憶

網站：bbs.21ic.com

BUCK 電路輸出一般只需要一級LC濾波器，

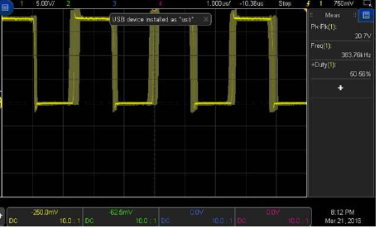
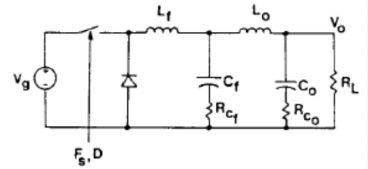
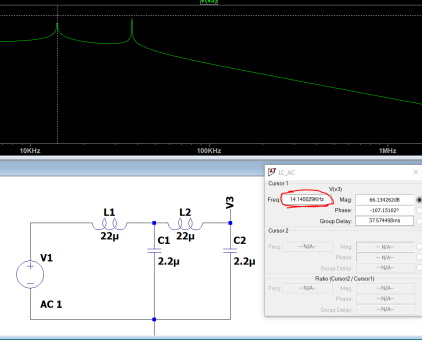
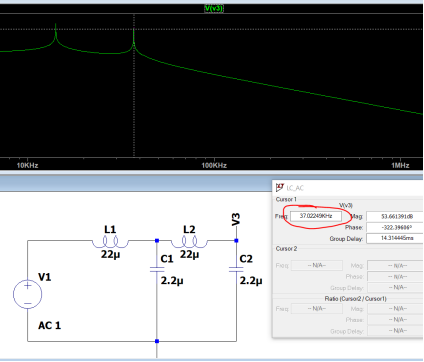
根據傳遞函數得知,會產生兩個極點和180°相移，司機對于干擾噪聲有-40dB/10dec的精品計衰減能力。對于特定產品在RE測試時候，原創有老尤其是兩級濾波路設車載產品，RF的器電限定標準嚴苛，濾波效果不好，司機很容易下高頻處超標。就需要用兩級LC濾波器。實現-80dB/10dec的衰減能力。但是使用兩級的LC濾波器，兩個濾波器的極點相互干擾，容易引起環路不穩定的情形發生，尤其是第二級LC濾波器的諧振頻率太靠近第一級LC濾波器的諧振頻率，就會造成輸出波形振蕩的狀況發生。在我的實際調試同行如下圖顯示，兩級LC濾波器的諧振頻率靠的太近，造成PWM開關頻率的波形開始振蕩。

根據大量經驗公式，第二級LC濾波器的諧振頻率fh要大于第一級LC濾波器的諧振頻率fl十倍以上，這樣系統環路才穩定的。當然，這個十倍的關系，可以通過優化layout，電感電容寄生參數優化，可以根據實際的調試結果減小，這個不是絕對值。

現在關鍵的部分來了，如何確定fh和fl的參數。

根據國外電源控制系統專家RIDLEY的文章，這兩級LC濾波器，假設Rcf=Rco=0，負載開路Rl=∞，利用文章的介紹，利用mathCAD我重寫了傳遞函數,可以得到：

其中wp為第一級LC濾波器的角頻率，wf為第二級LC濾波器的角頻率。因此可以得到第一級濾波器的諧振頻率fl：

? ?? ??

?第二級濾波器的諧振頻率fh：

通過公式可以看出，fl被兩級濾波器并聯電容和大電感決定的，fh被兩級濾波器串聯電容和小電感決定的。但是通過實際仿真，是假定Cf＞＞Co的情形下，fl和fh符合公式的。這個諧振頻率的公式在很多地方都直接引用看。

但是利用具體參數分別實際計算和仿真，就能防線這個公式是有一定局限性的。以下有實際電感電容來計算和仿真：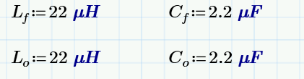

? ??

? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ?? ??

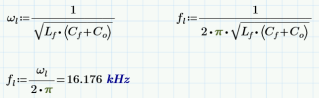通過仿真可以看出，仿真和matchCAD計算相差有相當的差距。但是只要Cf＞＞Co的條件滿足，一般這個差距就會縮小，感興趣的可以仿真驗證的。所以RIDLEY大神的文章中提及的公式是經過化簡的，需要滿足一定條件的，所以我嘗試寫出完整的傳遞函數，利用 EET（extra element theorem）重寫原始傳遞函數，

對公式進行化簡可以得到兩級濾波器的角頻率，詳細推導過程感興趣的可以自己推導的。新推導的兩個角頻率公式在滿足Cf＞＞Co的情形下，通過歸一化處理，可以得到和RIDLEY文章中一樣的結果。?這個新推導的諧振頻率公式在現有的論文文獻中還沒出現，說不定是全網首發呢，哈哈。但是由于第二級LC濾波器的諧振頻率要高于第一級濾波器諧振頻率的十倍以上，考慮到電感的成本效率等因素，因此第二級LC濾波器的電容會比第一級LC濾波器的電容小多了，所以RIDLEY文章中提到的諧振頻率公式是完全適用的，和我推導出的公式計算的結果是一樣的。

隨后我通過新推導的諧振頻率的兩個公式，再次帶入上文中用到的參數，得到兩級濾波器的諧振頻率。和仿真結果達到了完全一致的。因此適用面更廣泛的。

? ?

利用這兩個公式，在設計兩級濾波器的時候，可以知道電感電容對諧振頻率的影響。如果要保證第一次諧振頻率不變，但要拉大一二級濾波器諧振頻率的距離（保證系統穩定性），可以知道如何選擇電感電容的參數。對于電容負載電感負載對諧振頻率的影響，感興趣的小伙伴可以參考RIDLEY的文章-《Secondary LC Filter Analysis and Design Techniques for Current-Mode-Controlled Converters》《2 second stage filter design》，會大有裨益的。這個文章是自己一點心得，寫的不對還請大家多多指正。

出品：kk的回憶

---

免責聲明：本文內容由21ic獲得授權后發布，版權歸原作者所有，本平臺僅提供信息存儲服務。文章僅代表作者個人觀點，不代表本平臺立場，如有問題，請聯系我們，謝謝！
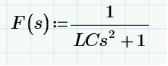
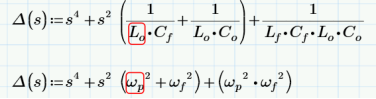
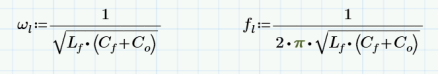
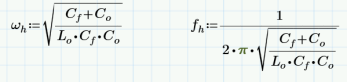
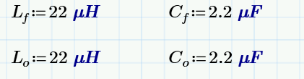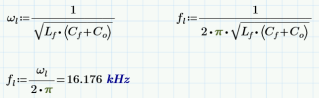
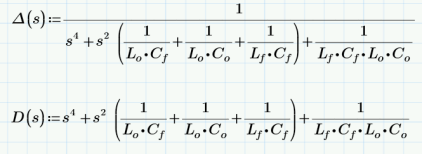
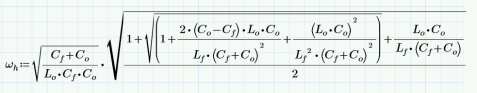
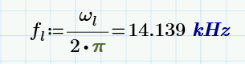
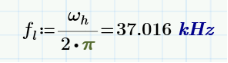
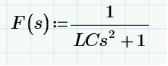
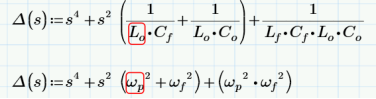
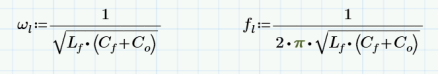
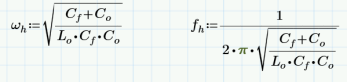
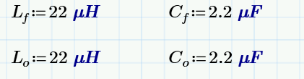